To calculate the weighted average interest rate of all your loans, multiply each loan amount by its interest rate. Add the results together, then divide that number by the sum of all your loan balances. Whatever that figure is, round up to the nearest 1/8 of a percent.
If you want to combine your federal loans together, the Direct Consolidation Loan program uses a weighted average interest rate. This becomes your new rate for the life of your consolidation loan, which can be a really long time (maybe 15 or 20 years, or even longer).
Note that federal consolidation is not your only option. In fact, it may not even be your best option. Student loan refinancing (through a private lender) is the only way to actually lower your interest rate. Refinancing also allows you to combine both federal and private loans together, as well as release cosigners on your loans. And if you are a parent who borrowed on behalf of your son or daughter, you may even be able to transfer your loan(s) to your child. Learn more about student loan refinancing.
What Is a Weighted Average Interest Rate?
It means that your interest rate will be based on the interest rates of the loans you would like to consolidate. And your highest outstanding federal loan balance will have the biggest impact on what your consolidation interest rate will be. The bigger the loan, the more ‘weight’ it will have on the interest rate calculation. It may push your consolidation interest rate a little higher or lower, but it likely won’t change much. After your weighted average interest rate is determined, the final step is to round up to the nearest 1/8th of 1 percent (.125). That is how the Direct Consolidation Loan program works.
Mathematical Background
Let I1, I2, …, In be the interest rates on n loans with balances B1, B2, …, Bn. The weighted average interest rate is
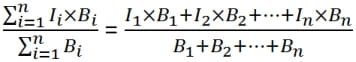
Example: Calculating Weighted Average Interest Rate
| Loan Balance | Interest Rate | |
|---|---|---|
| Loan #1 | $20,000 | 6.80% |
| Loan #2 | $10,000 | 7.90% |
| Loan #3 | $10,000 | 5.41% |
Step 1
Multiply each loan amount by its interest rate to obtain the per loan weight factor.
$20,000 * 6.80% = $1,360
$10,000 * 7.90% = $790
$10,000 * 5.41% = $541
Step 2
Add the per loan weight factors together to obtain the total per loan weight factor.
$1,360 + $790 + $541 = $2,691
Step 3
Add the loan amounts together to obtain the total loan amount.
$20,000 + $10,000 + $10,000 = $40,000
Step 4
Divide the total per loan weight factor by the total loan amount. Multiply this by 100 to express it as a percentage. This will give you the actual interest rate.
$2,691 / $40,000 = 6.7275%
Step 5
Then round the result to the next nearest 1/8%.
6.7275% rounded up to the nearest 1/8% = 6.75%
Thus the interest rate on the consolidation loan that combined these three loans would then be 6.75%.
Notice that this interest rate is above the lowest interest rate and below the highest interest rate. The weighted average interest rate is always between the highest and lowest interest rates.
Student Loan Repayment Relief
Need Help Paying Your Student Loans? Edvisors is giving out $2,500 in Student Loan Repayment Relief! If you would like a chance to win $2,500 towards paying down your student loans, make sure you enter!
- One winner per quarter.*
- Quick and easy form.











